Definition
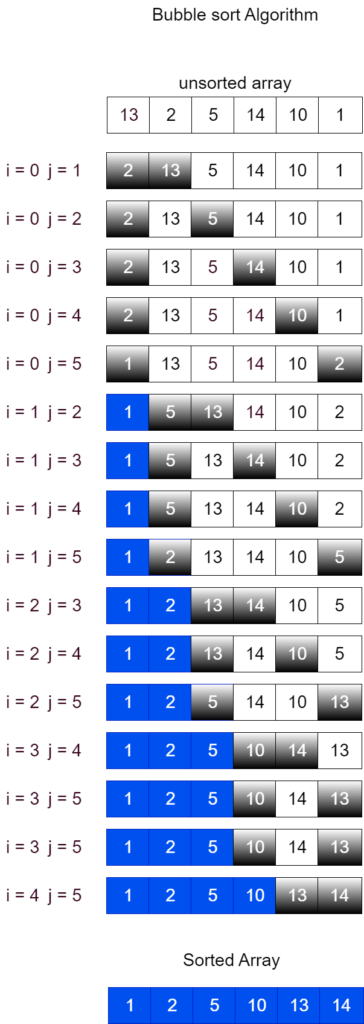
Bubble Sort Algorithm is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in the wrong order. This algorithm is not suitable for large data sets as its average and worst-case time complexity is quite high.
Flowchart of bubble sort algorithm
How bubble sort algorithm works?
Follow the below steps to solve the problem:
- Run a nested loop to traverse the input array using two variables i and j, such that 0 ≤ i < n-1 and 0 ≤ j < n-i-1
- If arr[j] is greater than arr[j+1] then swap these adjacent elements, else move on
- Print the sorted array
Below is the implementation of the above approach:
Non Optimized Implementation
Code implementation of bubble sort algorithm
Golang
package main
import (
"fmt"
)
// non optimized bubbleSort algorithm
func bubbleSort(arr []int) {
for i := 0; i < len(arr)-1; i++ {
for j := i + 1; j < len(arr); j++ {
if arr[i] > arr[j] {
arr[i], arr[j] = arr[j], arr[i]
}
}
fmt.Println(arr)
}
}
func main() {
arr := []int{13, 2, 5, 14, 10, 1}
fmt.Println("before bubble sort:", arr)
bubbleSort(arr)
fmt.Println("after bubble sort:", arr)
}Python
# non optimized bubble sort algorithm
def bubblesort(arr):
for i in range(len(arr)-1):
for j in range (i+1, len(arr)):
if arr[i] > arr[j]:
arr[i],arr[j] = arr[j],arr[i]
print(arr,end="\n")
arr = [23, 4, 23, 3, 24, 5, 65, 6, 9]
print("before bubble sort",arr, end="\n")
bubblesort(arr)
print("after bubble sort",arr,end="\n")
Javascript
// non optimized bubble sort algo in javascript
var bubblesort = (arr) => {
for (var i = 0; i < arr.length - 1; i++) {
for (var j = i + 1; j < arr.length; j++) {
if (arr[i] > arr[j]) {
// swap the values
var temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
console.log(arr)
}
}
var arr = [23, 4, 23, 3, 24, 5, 65, 6, 9];
console.log("before bubble sort", arr);
bubblesort(arr);
console.log("after bubble sort", arr)C Language
// Unoptimized implementation of Bubble sort
#include <stdio.h>
/* Function to print an array */
void printArray(int arr[], int size) {
int i;
for (i = 0; i < size; i++)
printf("%d ", arr[i]);
printf("\n");
}
void swap(int *xp, int *yp) {
int temp = *xp;
*xp = *yp;
*yp = temp;
}
// unoptimized version of Bubble Sort
void bubbleSort(int arr[], int n) {
int i, j;
for (i = 0; i < n - 1; i++) {
for (j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
swap(&arr[j], &arr[j + 1]);
}
}
printArray(arr, n);
}
}
// Driver program to test above functions
int main() {
int arr[] = {23, 4, 23, 3, 24, 5, 65, 6, 9};
int n = sizeof(arr) / sizeof(arr[0]);
printf("before bubble sort: ");
printArray(arr, n);
bubbleSort(arr, n);
printf("after bubble sort: ");
printArray(arr, n);
return 0;
}
C++
#include <bits/stdc++.h>
using namespace std;
// Function to print an array
void printArray(int arr[], int size) {
int i;
for (i = 0; i < size; i++)
cout << " " << arr[i];
cout << "\n";
}
// unoptimized version of Bubble Sort
void bubbleSort(int arr[], int n) {
int i, j;
for (i = 0; i < n - 1; i++) {
for (j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr[j], arr[j + 1]);
}
}
printArray(arr, n);
}
}
// Driver program to test above functions
int main() {
int arr[] = {23, 4, 23, 3, 24, 5, 65, 6, 9};
int N = sizeof(arr) / sizeof(arr[0]);
cout << "before bubble sort: ";
printArray(arr,N);
bubbleSort(arr, N);
cout << "after bubble sort: ";
printArray(arr, N);
return 0;
}
Output:
before bubble sort: [13 2 5 14 10 1]
[1 13 5 14 10 2]
[1 2 13 14 10 5]
[1 2 5 14 13 10]
[1 2 5 10 14 13]
[1 2 5 10 13 14]
after bubble sort: [1 2 5 10 13 14]
Time Complexity: O(N2)
Auxiliary Space: O(1)
Optimized Implementation of Bubble Sort Algorithm
The above function always runs O(N2) time even if the array is sorted. It can be optimized by stopping the algorithm if the inner loop didn’t cause any swap.
Below is the implementation for the above approach:
Golang
package main
import (
"fmt"
)
// optimized bubbleSort algorithm
func bubbleSort(arr []int) {
for i := 0; i < len(arr)-1; i++ {
swapped := false
for j := i + 1; j < len(arr); j++ {
if arr[i] > arr[j] {
arr[i], arr[j] = arr[j], arr[i]
swapped = true
}
}
fmt.Println(arr)
if swapped == false {
break
}
}
}
func main() {
arr := []int{13, 2, 5, 14, 10, 1}
fmt.Println("before bubble sort:", arr)
bubbleSort(arr)
fmt.Println("after bubble sort:", arr)
}
Python
# optimized bubble sort algorithm
def bubblesort(arr):
for i in range(len(arr)-1):
swapped = False
for j in range (i+1, len(arr)):
if arr[i] > arr[j]:
arr[i],arr[j] = arr[j],arr[i]
swapped = True
print(arr,end="\n")
if swapped == False:
break
arr = [23, 4, 23, 3, 24, 5, 65, 6, 9]
print("before bubble sort",arr, end="\n")
bubblesort(arr)
print("after bubble sort",arr,end="\n")
Javascript
// optimized bubble sort algo in javascript
var bubblesort = (arr) => {
for (var i = 0; i < arr.length - 1; i++) {
var swapped = false;
for (var j = i + 1; j < arr.length; j++) {
if (arr[i] > arr[j]) {
// swap the values
var temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
swapped = true;
}
}
console.log(arr);
if (!swapped) {
break
}
}
}
var arr = [23, 4, 23, 3, 24, 5, 65, 6, 9];
console.log("before bubble sort", arr);
bubblesort(arr);
console.log("after bubble sort", arr)
C Language
// Optimized implementation of Bubble sort
#include <stdbool.h>
#include <stdio.h>
/* Function to print an array */
void printArray(int arr[], int size) {
int i;
for (i = 0; i < size; i++)
printf("%d ", arr[i]);
printf("\n");
}
void swap(int *xp, int *yp) {
int temp = *xp;
*xp = *yp;
*yp = temp;
}
// An optimized version of Bubble Sort
void bubbleSort(int arr[], int n) {
int i, j;
bool swapped;
for (i = 0; i < n - 1; i++) {
swapped = false;
for (j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
swap(&arr[j], &arr[j + 1]);
swapped = true;
}
}
printArray(arr, n);
// IF no two elements were swapped by inner loop, then break
if (swapped == false)
break;
}
}
// Driver program to test above functions
int main() {
int arr[] = {23, 4, 23, 3, 24, 5, 65, 6, 9};
int n = sizeof(arr) / sizeof(arr[0]);
printf("before bubble sort: ");
printArray(arr, n);
bubbleSort(arr, n);
printf("after bubble sort: ");
printArray(arr, n);
return 0;
}C++
// Optimized implementation of Bubble sort
#include <bits/stdc++.h>
using namespace std;
// Function to print an array
void printArray(int arr[], int size) {
int i;
for (i = 0; i < size; i++)
cout << " " << arr[i];
cout << "\n";
}
// An optimized version of Bubble Sort
void bubbleSort(int arr[], int n) {
int i, j;
bool swapped;
for (i = 0; i < n - 1; i++) {
swapped = false;
for (j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr[j], arr[j + 1]);
swapped = true;
}
}
printArray(arr, n);
// IF no two elements were swapped
// by inner loop, then break
if (swapped == false)
break;
}
}
// Driver program to test above functions
int main() {
int arr[] = {23, 4, 23, 3, 24, 5, 65, 6, 9};
int N = sizeof(arr) / sizeof(arr[0]);
cout << "before bubble sort: ";
printArray(arr, N);
bubbleSort(arr, N);
cout << "after bubble sort: ";
printArray(arr, N);
return 0;
}
Output:
before bubble sort: [13 2 5 14 10 1]
[1 13 5 14 10 2]
[1 2 13 14 10 5]
[1 2 5 14 13 10]
[1 2 5 10 14 13]
[1 2 5 10 13 14]
after bubble sort: [1 2 5 10 13 14]
Time Complexity: O(N2)
Auxiliary Space: O(1)
Worst Case Analysis for Bubble Sort Algorithm
The worst-case condition for bubble sort occurs when elements of the array are arranged in decreasing order.
In the worst case, the total number of iterations or passes required to sort a given array is (n-1). where ‘n’ is a number of elements present in the array.
At pass 1 : Number of comparisons = (n-1)
Number of swaps = (n-1)
At pass 2 : Number of comparisons = (n-2)
Number of swaps = (n-2)
At pass 3 : Number of comparisons = (n-3)
Number of swaps = (n-3)
.
.
.
At pass n-1 : Number of comparisons = 1
Number of swaps = 1
Now , calculating total number of comparison required to sort the array
= (n-1) + (n-2) + (n-3) + . . . 2 + 1
= (n-1)*(n-1+1)/2 { by using sum of N natural Number formula }
= n (n-1)/2 For the Worst case
Total number of swaps = Total number of comparison
Total number of comparison (Worst case) = n(n-1)/2
Total number of swaps (Worst case) = n(n-1)/2
Worst and Average Case Time Complexity: O(N2). The worst case occurs when an array is reverse sorted.
Best Case Time Complexity: O(N). The best case occurs when an array is already sorted.
Auxiliary Space: O(1)
Recursive Implementation Of Bubble Sort Algorithm
Golang
package main
import (
"fmt"
)
func recursiveBubbleSort(arr []int, length int) {
if length == 0 || length == 1 {
return
}
for i := 0; i < length-1; i++ {
if arr[i] > arr[i+1] {
arr[i], arr[i+1] = arr[i+1], arr[i]
}
}
fmt.Println(arr)
recursiveBubbleSort(arr, length-1)
}
func main() {
arr := []int{13, 2, 5, 14, 10, 1}
fmt.Println("before bubble sort:", arr)
recursiveBubbleSort(arr)
fmt.Println("after bubble sort:", arr)
}
Live Codebase Links are mentioned below:
Golang
Please write comment if you find anything wrong, or if you want to share more information about the topic explained in this post.

